ADVERTISEMENTS:
After reading this article you will learn about the axil characters of different crystal systems.
Elements of Crystals and their Interrelationship:
Elements of crystals such as:
(a) Face (F),
ADVERTISEMENTS:
(b) Edge (E), and
(c) Solid angle (A).
1. Face:
Faces are the plain surfaces of the crystals.
2. Edge:
ADVERTISEMENTS:
Edges are borders formed by the intersection of any two faces.
ADVERTISEMENTS:
3. Solid angle:
Solid angles are the corners formed by the intersection of three or more faces or edges.
The relationship of these faces, edges and solid angles are governed by a formula known as Euler’s formula.
Euler’s formula says that:
F + A = E + 2
where,
F = number of faces in a crystal
A = number of solid angles
E = number of edges in a crystal
ADVERTISEMENTS:
2 = constant
Example:
Crystallographic Axes:
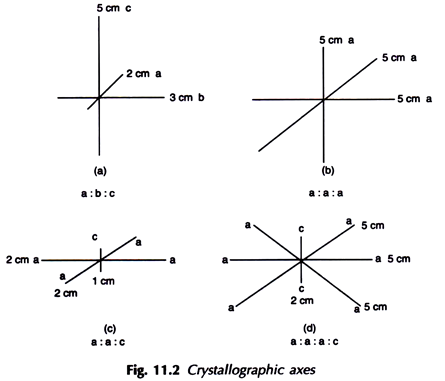
Crystallographic axes are imaginary lines of reference converging at the center of a crystal generally occupying the three important positions in a crystal such as front to back, side to side and top to bottom, They are mentioned with algebraic letters a, b and c respectively. If all the three crystallographic axes are unequal then the symbol or (Weiss) Notation will be a: b: c [Fig. 11.2(a)].
Example:
Orthorhombic System,
Monoclinic System, and
Triclinic System.
If the entire three crystallographic axes are equal it is written as a: a: a [Fig. 11.2(b)].
Example:
Isometric System.
If any two crystallographic axes which are equal and interchangeable it will be a: a: c [Fig. 11.2(c)].
Example:
Tetragonal System.
But in the case of Hexagonal system the crystal possess four crystallographic axes three equal and interchangeable with one unequal being the vertical axis the symmetry is represented as a : a : a : c [Fig. 11.2(d)],
Example:
Hexagonal System.
Based on the crystallographic axis all the crystals are classified into six different crystal systems such as:
1. Isometric System,
2. Tetragonal System,
3. Hexagonal System,
4. Orthorhombic System,
5. Monoclinic System, and
6. Triclinic System.
Note:
α is the angle between b and c.
β is the angle between a and c.
χ is the angle between a and b.
Axial and Symmetry Characters:
1. Axial Characters of Isometric System:
In this system there are three crystallographic axes. All the three crystallographic axes which are equal and interchangeable cut at 90°, therefore, the symbol is a: a: a and the axial angle is∠a ∠a ∠a = 90° [Fig. 11.3(a)].
Example:
Halite.
2. Axial Characters of Tetragonal System:
In this system there are three crystallographic axes, among these two crystallographic axes (Front to Back and Side to Side) which are equal and interchangeable. The third crystallographic axes (vertical crystallographic axis) which is unequal (it may be bigger or smaller) therefore the symbol is a: a: c and the axial angle is ∠a ∠a ∠c = 90° [Fig. 11.3(b)],
Example:
Zircon.
3. Axial Characters of Hexagonal System:
In this system there are four crystallographic axes. Three crystallographic axes which are equal and interchangeable cut at 60° or 120°. The fourth one that is vertical crystallographic axis which is unequal (it may be bigger or smaller), therefore, the symbol is a: a: a: c and the axial angle is ∠a ∠a = 60° or 120°, ∠a ∠c = 90° [Fig. 11.3(c)],
Example:
Quartz.
4. Axial Characters of Orthorhombic System:
In this system there are three crystallographic axes. All the three crystallographic axes, which are unequal in length and cut at 90°, therefore, the symbol is a : b : c and the axial angle is ∠a ∠b ∠c = 90° [Fig. 11.3(d)],
Example:
Staurolite.
5. Axial Characters of Monoclinic System:
In this system there are three crystallographic axes. All the three crystallographic axes, which are unequal in length. Therefore, the symbol is a: b: c and the axial angle is ∠a ∠c = 90°, ∠b ∠c = 90°, ∠a ∠c not equal to 90° [Fig. 11.3(e)].
Example:
Orthoclase.
6. Axial Characters of Triclinic System:
In this system there are three crystallographic axes. All the three crystallographic axes, which are unequal in length and not cut at 90°, therefore, the symbol is a :b : c and the axial angle is ∠a ∠a ∠c not equal to 90° [Fig. 11.3(f)].
Example:
Albite.
Symmetry Characters:
Symmetry is defined as the similar arrangement of crystal elements in a crystal.
Symmetry may be defined in relation to the following three important factors:
(i) Centre of Symmetry:
In a crystal if for each face, edge or solid angle there occurs an exactly similar face, edge or solid angle at the same distance away from the center on its diametrically opposite side indicates the presence of center of symmetry.
(ii) Plane of Symmetry:
When a crystal is divided into two equal halves, one half is the mirror image to the other half. Or one half is the reflection to the other half.
The plane of symmetry is further divided into two types:
(a) Principle Plane of Symmetry (PPS).
(b) Secondary Plane of Symmetry (SPS).
(a) Principle Plane of Symmetry:
If the plane of symmetry passes through two or more equal and interchangeable crystallographic axes. The plane of symmetry is described as principle plane.
(b) Secondary Plane of Symmetry:
If the plane of symmetry does not through two or more equal and interchangeable crystallographic axes then the plane of symmetry is described as secondary plane.
(iii) Axis of Symmetry:
When a crystal is rotated to an angle of 360° similar faces may come and occupy the same position in space more than once in a complete rotation. The axis of symmetry depending upon the number of similar faces repeated in a rotation of 360°.
If the similar faces repeated twice then the axis of symmetry is called two fold or digonal.
If the similar faces repeated thrice then the axis of symmetry is called three fold or trigonal.
If the similar faces repeated four times then the axis of symmetry is called four fold or tetrad.
If the similar faces repeated six times then the axis of symmetry is called six fold or hexad.
Note:
CS = Centre of Symmetry.
PPS = Principle Plane of Symmetry.
SPS = Secondary Plane of Symmetry.
(ii), (iii), (iv) and (vi) = two fold, three fold, four fold and six fold axis of symmetry
CA = Crystallographic Axes.
Interfacial Angle (IFA):
Interfacial angle is angle between any two adjacent faces of a crystal. The instrument used to measure interfacial angle is called Contact Goniometer.
Contact Goniometer:
The interfacial angles of crystals are measured by means of instrument, which is called Contact Goniometer (Fig. 11.4).
The instrument consists of graduated arc, indicator and the base and a screw. The base and the arm are brought accurately into contact with the two adjacent faces of a crystal. In the illustration the angle actually measured is the internal angle between the two adjacent faces of a crystal-IFA.
Weiss Notation:
Weiss invented this system in the year 1818. He makes use of parameter values to express the notation. Parameters the intersect made by the face on crystallographic axes.
If all the three crystallographic axes are equal then the Weiss notation is a: a: a. If they are unequal he use a to the front to back b to the side to side and c to the vertical axes.
In orthorhombic system the front to back crystallographic axes is called the Brachy axis and indicated by the symbol ă and the side to side crystallographic axes is called the Macro axis and indicated by the symbol b̅ .
In monoclinic system the front to back crystallographic axes is called the clinoaxis and indicated by the symbol a and side to side axis is called the ortho axis and indicated by the symbol b.
In triclinic system the front to back crystallographic axes is called the Brachy axis and indicated by the symbol a̅ and side to side crystallographic axes is called the Macro axis and indicated by the symbol b.
The actual letters the second should be maintained as unity indicates the parameter values.
The ratio dots should be maintained. If the particular face does not meet the axis then infinity should be maintained.