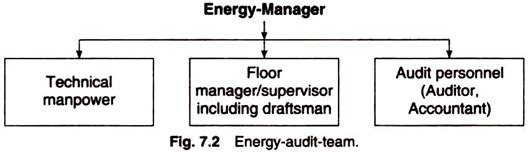
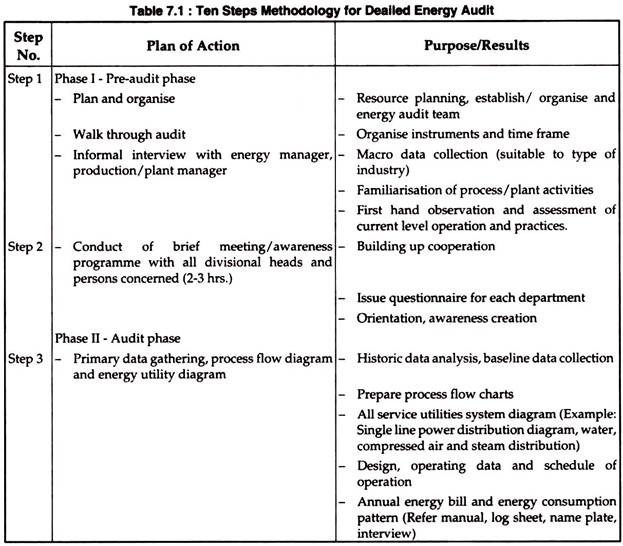
ADVERTISEMENTS:
Accurate computation of runoff amount from a watershed is difficult, as it depends on several factors concerned with the atmosphere and watershed characteristics, to evaluate which effect on runoff is not so easy.
On the basis of field experiences and observations, the following methods are frequently used in the field of soil and water conservation for estimating the maximum or peak runoff rate of a particular watershed to design the soil and water conservation structures:
1. Rational Method:
This is a most common method used to compute the peak runoff rate from the small watershed. The peak runoff is defined as the maximum runoff to be used as capacity for design of a given structure that must carry the runoff.
ADVERTISEMENTS:
Rational method involves following formula for computing the design runoff:
Where,
Qpeak = peak runoff rate, m3/s
C = runoff coefficient
ADVERTISEMENTS:
I = rainfall intensity (mm/h) for the duration equal to time of concentration of watershed and for a given recurrence interval
A = watershed area, hectare.
Assumptions of Rational Method:
ADVERTISEMENTS:
The Rational formula involves following assumptions:
i. Rainfall occurs with a uniform intensity for the duration at least equal to the time of concentration of watershed; and
ii. Rainfall occurs at a uniform intensity throughout the watershed area.
If all these assumptions are satisfied to a given rainfall, then the relationship between rainfall and runoff for the watershed is being most accurate. Graphically, the relationship between rainfall and runoff is shown in Fig. 2.2.
Fig. 2.2. Indicates that if a specific rainfall of uniform intensity occurs for the duration greater than the time of concentration, then peak runoff remains same. On the other hand a rain that takes place for the duration less than the time of concentration, the runoff rate will be less than peak value, because the entire watershed area would not be able to yield the discharge, simultaneously to the outlet.
a. Runoff Coefficient (C):
Runoff coefficient is the fraction of rainfall converting into surface runoff. It is defined as the ratio of the runoff and rainfall. It is a dimensionless factor. Its value depends on the land use and soil types (Table 2.1)
The C values vary from close to zero to 1.0. A low C value indicates that, most of the rain water is soaking into the ground or very little formation of runoff, whereas a high C value denotes that, most of the rain water is retained on the ground surface which gets converted into runoff. The sandy or tilled areas have low C values. The paved surfaces or other impermeable surfaces have a high C value. Also, the steep soil surface involves greater value of C, as there less water is retained or soaked into the soil.
If a watershed has different features regarding its land use and soil types, then weighted value of runoff coefficient is calculated. A sample example for computing the weighted runoff coefficient is shown as under – Let, a watershed has been divided into five sub parts on the basis of its soil types and land use, having the area a1, a2, a3, a4 and a5, with the values of runoff coefficient c1, c2, c3, c4 and c5, respectively.
The value of weighted runoff coefficient ‘C’ is given by-
In which, A is the total area of watershed.
b. Rainfall Intensity:
It is defined as the rate of fall of rainfall, expressed as depth per unit time, i.e., mm/hour. It is also expressed as the ratio of total amount of rainfall to its duration.
It is given by-
In which, I is the rainfall intensity, P is the amount of rainfall and T is the duration of rainfall. In rational method to compute peak runoff rate, the rainfall duration should at least be equal to the time of concentration (i.e., time required to move the surface flow from remotest point of the watershed to the outlet) for producing peak runoff from watershed.
Rainfall intensity is classified into following three categories:
(1) Light Intensity — 2.5 mm/h
(2) Moderate Intensity — 2.5 to 7.5 mm/h
(3) Heavy Intensity — more than 7.5 mm/h
c. Time of Concentration (Tc):
The time required to move the surface runoff from remotest point of the watershed to its outlet is known as time of concentration. When duration of rainfall becomes equal to the time of concentration, then all parts of the watershed become able to generate the discharge to the outlet, simultaneously; and the cumulative discharge at the outlet takes the form of maximum runoff which is referred as peak runoff.
d. Computation of Time of Concentration:
There have been developed several empirical relations for computing the time of concentration. Kirpich (1940) developed following equation for computing the Tc on the basis of channel length and its average slope, is very common.
The equation is given as:
Where,
Tc = time of concentration, minutes
L = Length of channel reach, m.
S = average slope of the channel reach, m/m.
Haan et al. (1982) mentioned that, the above relationship does not give accurate value of time of concentration for the watersheds less than 5 sq. km area. He justified that the small watersheds are dominated by overland flow rather than channel flow.
To account this effect, he modified the above equation, considering the effect of overland flow on Tc, given as:
Where,
L0 = length of overland flow, m
n = Manning’s roughness coefficients (Table 2.2)
S0 = slope of the flow path, m/m.
In above equation (i.e., eq. 2.10) the second term accounts the overland flow. It has been reported from several field and laboratory studies, that the overland flow has a maximum travel time and can be maintained up to a distance of 100 to 150 meters in the watershed. Thus, the value of second term can be a maximum regardless of watershed size.
However, the channel length increases with increase in the size of watershed, which indicates that as the size of watershed increases, the time of concentration also increases, which will affect the overall value of surface runoff. The effect of all these points on runoff has been incorporated in equation 2.10. In this way the eq. 2.10 is valid for all size of the watersheds for computing Tc.
In above equation, it was assumed that the time of concentration is approximately equal to the lag time of the peak flow.
e. One Hour Rainfall:
The intensity of severest rainfall during a given recurrence interval of a particular region, for the time interval of one hour is called one hour rainfall for that return period/frequency. In the Rational method for computing the peak runoff, the intensity of rainfall should be for the time equal to the time of concentration. In this case one hour rainfall intensity is converted accordingly with Tc value. For this purpose Fig. 2.3 may be used.
Limitations of Rational Method:
Following limitations are observed in use of rational method:
i. Rational method assumes that the intensity of rainfall is uniformly distributed throughout the watershed, but it never happen.
ii. This method does not care the initial losses such as depression storage, initial infiltration, channel storage etc.
iii. The runoff co-efficient value is related as the function of watershed characteristics such as land use, topography soil types etc., do not provide correct value. The runoff coefficient also depends on the atmospheric characteristics like, season and rainfall etc.
2. Cook’s Method:
This method consists of evaluating the four watershed characteristics, i.e., relief, infiltration rate, vegetal cover and surface storage to determine the runoff rate. For these individual characteristics, numerical values are assigned. Numerical values are mainly given on the basis of observation and comparison of their features with the similar conditions of the watershed. The numerical values of above four characteristics based on their relative conditions are given in the Table 2.4.
For computation of runoff the next-step is to obtain the sum of numerical values assigned for all four characteristics (ΣW) and then computing uncorrected runoff by using the runoff curve, shown in Fig. 2.5, against the sum of the numerical value. The runoff determined so is valid for 10 years recurrence interval. Again this value of runoff is modified for geographic location of the given watershed and for the desired recurrent interval.
This is done by using the following formula:
Q = PRFS …..(2.14)
Where,
Q = peak runoff rate for a specified geographic location and desired recurrence interval.
P = uncorrelated value of runoff, i.e., obtained from the runoff-curve.
R = geographic rainfall factor.
F = recurrence interval factor.
S = shape factor of the watershed.
The computation of peak runoff by this method is shown in example 2.9.
3. Curve Number Method:
It computes the direct runoff (depth) or rainfall excess, storm-wise. This method is based on the potential retention capacity (S) of the water-shed., which is determined based on the wetness of the watershed, i.e. the antecedent moisture condition and physical characteristics of the watershed.
Let ‘Ia’ is the initial loss of rain water by interception, infiltration through the soil, depression storage etc. The initial losses are satisfied by the rainfall before starting of the runoff. This method assumes that the ratio of direct runoff (surface runoff) (Q) to the rainfall depth minus the initial losses (P—Ia) is equal to the ratio of actual retention of rainfall to the S, i.e.
In which, CN is the curve number. Its value varies from minimum zero for the most permeable surface to the maximum 100 for impervious (concrete) surface. The values of curve number for different land use conditions and hydrologic soil groups are given in Table 2.5.
These values are applied to the antecedent moisture condition II only, i.e., for average condition. To get the CN values for other AMCs (i.e., I and III), the correction factors are applied. The values of correction factors for other antecedent moisture conditions are given in Table 2.6. The equation (2.16) estimates the value of runoff (Q) in depth unit.
Antecedent Moisture Content (AMC):
It is used as the wetness index of soil.
There are three levels of AMC, given as under:
AMC I. This includes the lowest runoff potential, because the soils are dry enough for satisfactory cultivation to take place.
AMC II. In includes average condition of the soil regarding runoff generating potential.
AMC III. This includes the features favourable to develop highest runoff potential of the soil, when areas of watershed are saturated from antecedent rains.
The AMC is determined on the basis of 5-days antecedent rainfall amounts.