How to Estimate the Future Population?: Factors and Methods | Geography

A water supply project is planned to meet the present requirements as well as the requirements for a reasonable future period termed as the design period. As such it is essential to know the present population of the town or city and also to forecast or estimate the future population. The information about the population of a town or city at any time may be obtained from the census records.

The census is usually conducted by the central government at an interval of 10 years, which is thus termed as decennial census. However, sometimes additional information about the population may also be obtained by conducting special surveys by state governments or some local bodies in between the two census years.

The present population of a town or city may be obtained by extending the line of the last two preceding census figures upto the year in question. The future population of a town or city at the end of a design period may be predicted on the basis of the census data for a number of preceding census years.

However, in order to predict the future population, as correctly as possible, it is necessary to know the factors affecting the population growth.

Factors Affecting Population Growth:

The various factors mainly responsible for the variation in the population of a town or city are as follows:

(i) Birth rates

(ii) Death rates

(iii) Migration rates

These factors are considerably influenced by social and economic conditions of the existing population of the town or city. The effect of each of these factors on the population growth is as indicated below.

The population of a town or city increases with the increase in the birth rates and it decreases with the decrease in the birth rates. The birth rates may decrease due to excessive family planning practices and legalised abortions. Further the spread of education and development of various recreational facilities for the people also tend to reduce the birth rates.

The population of a town or city decreases with the increase in the death rates and vice versa. The death rates may decrease with the development and advancement of the medical facilities, thereby controlling the infant mortality rates as well as the adult death rates.

Due to large number of people migrating to a town or city, its population will increase. People generally migrate from villages to towns or cities where more opportunities for earning livelihood are available due to industrialisation and commercialisation of the towns or cities.

The migration rates and hence the population therefore tend to increase sharply with the development of industries and commercial activities in towns and cities. The migration rates may, however, decrease when immigration restrictions are imposed.

Besides the above indicated three factors, some other factors such as wars, natural havocs or disasters such as epidemics, earthquakes, etc., may also bring about sharp reductions in the populations of towns or cities.

On account of the varying influences of these factors on the population growth, the exact prediction of the future population by evaluating these factors is rather difficult. Therefore the prediction of the future population of a town or city is usually done by adopting mathematical formulae and graphical methods based upon the population data for a number of preceding census years.

Population Growth Curve:

It is evident that under normal circumstances the population of a town or city cannot increase indefinitely but it always tends to approach a saturation value or upper limit. As such when the varying influences of the various factors do not produce any extraordinary changes then the population would follow the growth curve which is characteristic of all forms of life within a limited space.

This curve as shown in Fig. 2.3 is S-shaped and it is known as logistic curve. The curve indicates an early growth of population taking place at an increasing rate from a to d, and a late growth of population at a decreasing rate from e to c, as a saturation value or upper limit is approached. From d to e the rate of growth of population is almost constant, being approximately a straight line increase.

If the population increase dP in the time interval dt is constant i.e., rate of growth of population dp/dt = a constant k_a, the population growth is arithmetic.

Integration between the limit P_m (the desired mid-year population) and P_e or P_l, and between the limits t_m (the desired date) and t_e or t_l, gives the mid-year population as follows:

The geometric estimates the logarithms of the populations are used, and in the arithmetic estimates the populations themselves are used; also that arithmetic increase is analogous to growth by simple interest, and geometric increase to growth by compound interest.

The lower portion of the S-shaped growth curve (Fig. 2.3), concave upward from a to d, is approximated by geometric increase, and the central portion, approximately straight line from d to e, is approximated by arithmetic increase. The upper portion of the curve, concave downward from e to c, is analogous to first order curve for which the rate of growth of population dp/dt ∝ (P_s – P), where P_s is the saturation value or upper limit of the population.

From Eq. 2.15 or 2.17 the future population may be estimated by using the population of the last two censuses. However, the estimates of the population so obtained may be true for only short-term forecasts, and the long-range forecasts of population made by using the population of only the last two censuses are not the true estimates of the future population. As such for long-range forecasts instead of dealing with the results of the last two censuses only, the full available record of a number of census years is used.

Methods for Estimating Future Population:

The various methods generally adopted for forecasting or estimating the future population are as indicated below:

(1) Arithmetical Increase Method:

In this method it is assumed that the future increase in population is at a constant rate. This constant rate of increase in population in future is taken as the average increase in population per decade during a number of past successive decades. Thus from the known populations of a number of past successive decades the increase in population during each decade is computed and from these the average increase in population per decade is worked out.

The average increase in population per decade is added for each successive future decade to obtain the prospective population of the corresponding future decade. As such if c is the average increase in population per decade then the prospective population P₁ after one decade from the year corresponding to the latest known population P₀ is given by the expression-

P₁ = P₀ + 1 × c

Similarly the prospective population P₂ after two decades from the year corresponding to the latest known population P₀ is given by the expression-

P₂ = P₁ + 1 × c

or P₂ = P₀ + 2c

Thus the prospective population P_n after n decades from the year corresponding to the latest known population P₀ is given by the expression-

P_n = P₀ + nc …(2.18)

This method, however, gives low results and it is to be adopted for large cities which have practically reached their maximum development.

(2) Geometrical Increase Method:

In this method it is assumed that the percentage increase in population per decade remains constant for each future decade. The value of this constant percentage increase in population per decade may be determined from the known populations of a number of past successive decades by different methods.

Thus if r is the percentage increase in population per decade (being constant for each future decade) then the prospective population P₁ after one decade from the year corresponding to the latest known population P₀ is given by the expression.

The value of r to be used in Eq. 2.19 may be determined from the known populations of a number of past successive decades by different methods as indicated below:

(i) According to one of the methods the value of r may be computed by the following expression

in which

P₀ = the latest known population in the series of population data used for prediction of future population;

P_i = the initial known population in the series of population data used for prediction of future population; and

t = number of decades between the populations P and P₀, or the number of decades of which the population data is used for prediction of future population.

(ii) In the other method, for the known populations of the number of past successive decades the percentage increase in population for each decade is first computed which is given as-

The value of r is then taken as either the arithmetic mean or the geometric mean of these percentage increase in population for each decade.

Thus if r₁, r₂, r₃,……. r_t, are the percentage increase in population for each of the past t successive decades then the value of r is taken as either the arithmetic mean of r_1, r₂, r₃, …r_t, i.e.,

It has been found that in general the value of r obtained by arithmetic mean is slightly higher than that obtained by geometric mean. However, the GOI Manual on Water and Water Treatment recommends the use of geometric mean for determining the value of r and hence the same is generally adopted.

The geometrical increase method usually gives higher results as compared to the arithmetical increase method. The geometrical increase method is generally considered suitable for old cities which are not undergoing further development.

(3) Incremental Increase Method:

In this method the population of each successive future decade is first worked out by the arithmetical increase method and to these values the average incremental increase per decade is added once for the first future decade, twice for the second future decade, thrice for the third future decade, and so on. The incremental increase per decade is defined as the difference between the increase in population during the successive decades.

Thus from the known populations of a number of past successive decades the increase in population during each decade is computed and from these the average increase in population per decade is worked out. Further from the increase in population during the past successive decades the incremental increase is computed.

The incremental increase may be positive or negative depending on the increase in the population during a successive decade is more than or less than the increase in the population during its preceding decade. From the computed values of the incremental increase the average incremental increase per decade is worked out. Thus if c is the average increase in population per decade and x is the average incremental increase per decade then the prospective population P₁ after one decade from the year corresponding to the latest known population P₀ is given by the expression.

This method embodies the advantages of both the arithmetical increase method and the geometrical increase method. The results given by this method are somewhere between the results given by the arithmetical increase method and the geometrical increase method, and hence the results given by this method are considered to be quite satisfactory.

(4) Changing Rate of Increase Method:

This method is similar to the geometrical increase method except that instead of a constant value of the percentage increase in population per decade a decreasing value of the percentage increase in population per decade is adopted for each future decade.

For determining the decreasing value of the percentage increase in population per decade for each future decade, the average decrease in the percentage increase in population per decade is worked out and it is subtracted from the latest percentage increase in population per decade for each successive future decade.

Thus from the known populations of a number of past successive decades the percentage increase in population for each decade is first computed. Then the difference in the percentage increase in population during the successive decades is computed and their average value is worked out which is taken as the average decrease in the percentage increase in population per decade for each future decade.

For example if r₁, r₂, r₃,……. r_t are the percentage increase in population for each of the past successive decades then the average decrease in the percentage increase in population per decade r’ is given by the expression

This method is considered suitable for large cities for which the population is approaching the saturation limit and in cases where the rate of growth is showing a downward trend.

(5) Graphical Method:

In this method the known populations of a number of past successive decades are plotted against the respective years of record and a smooth curve is drawn through the plotted points. The curve is then smoothly extended keeping in view the general trend of the curve as well as the past history of the city and the probable future conditions. The prospective population of each future decade is read from the extended curve.

For example the population of a particular city for the six decades from 1931 to 1991 is as noted below:

These are plotted as shown in Fig. 2.4 and the curve drawn through the plotted points is extended from which the prospective population for the year 2021 is obtained as 80 × 10³.

(6) Comparative Method or Curvilinear Method:

In this method it is assumed that the city whose future population is to be estimated will develop in the same manner as the other similar cities have developed in the past, and hence its future population growth will match with the past population growth of the similar cities.

Thus for the city whose future population is to be estimated, the known population of a number of past successive decades is plotted against the respective years of record upto the year corresponding to the latest known population and a smooth curve is drawn through the plotted points.

For obtaining the future population growth of the city the plotted population growth curve is extrapolated by comparison with the population growth of the other similar cities of larger size. The cities chosen for the comparison should be as far as possible similar to the city under consideration in respect of geographical proximity, economic base, access to transportation system, etc.

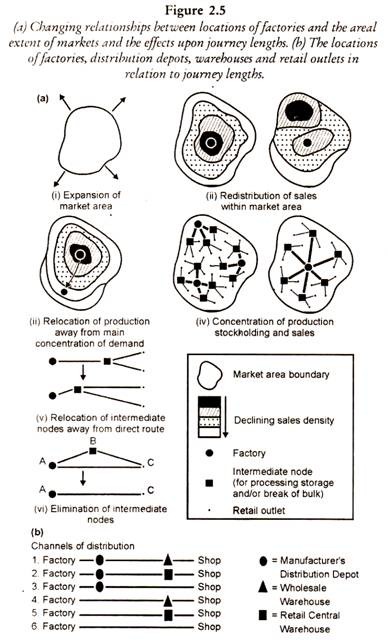
For example the future population growth is to be obtained for a city A for which the population upto the year 1971 is known, and the same is plotted as shown in Fig. 2.5.

The population growth curves of cities B, C, D and E start from the same point P which represents the latest known population year point on the population growth curve of city A. The population growth curve of city A is then extrapolated keeping in view the rates of growth of the cities B, C, D, and E as shown in Fig. 2.5. The estimated population of city A for each successive future decade may then be obtained from the extrapolated population growth curve for city A.

The comparative method is based on a logical background and hence if statistics of development of similar cities are available the results obtained by this method would be reliable and satisfactory.

(7) Decreasing Rate of Growth Method or Declining Growth Method:

In this method it is assumed that the city has some limiting saturation population and the rate of growth of population decreases as the size of the city increases. With this consideration the prospective population P_n after n decades from the year corresponding to the latest known population P₀ is given by the expression

in which

P₀ = the latest known population

P₁ = the population t₁ decades prior to the latest known population P₀; and

P₂ = the population t₁ decades prior to the population P₁ or 2t₁ decades prior to the latest known population P₀

The past populations P₁ and P₂ are so chosen that the time interval between the populations P₀ and P₁ is same as that between the populations P₁ and P₂, and this time interval may be one decade (in which case t₁ = 1 decade), or more than one decade depending upon the availability of the population data.

The value of the coefficient K’ may be determined by the following expression-

in which

P = any population recorded t decades after the population P₂ is recorded

Usually P may be taken equal to P_Q in which case t will be equal to the time interval in decades between the populations P₂ and P₀.

(8) Logistic Method:

This method is based on the assumption that the population growth of a city follows the logistic curve (Fig. 2.3), and hence the future population of a city may be predicted from the equation of the logistic curve.

According to P.F. Verhulst the entire logistic curve ac can be represented by the following equation:

Equation 2.30 may be used for the prediction of the future population as indicated below.

McLean has suggested that from the known populations of the past three successive census the values of P_s, m and b may be obtained. Thus if P₀ is the latest known population, P₁ is the population t₁decades prior to the latest known population P₀, and P₂ is the population t₁ decades prior to the population P₁ or 2t₁ decades prior to the latest known population P₀, then-

The values of P_s, m and b obtained by these equations when introduced in Eq. 2.30 permits the estimation of population for any period/beyond the base year corresponding to the population P₂.

Thus the population P_n after n decades from the year corresponding to the latest known population P₀ is given by Eq. 2.30 as-

since t = 10 (n + 2t₁) years, being the time interval in years between the populations P₂ and P_n.

(9) Zoning Method or Master Plan Method:

If a master plan of the city has been prepared then the future population of the city can be predicted on the basis of the prospective development as indicated in its master plan. In the master plan of the city it is divided into different zones such as residential zone, industrial zone, commercial zone, etc. The provisions in the master plan control the character of various zones and the city is allowed to develop in a definite way.

Thus by assuming suitable population densities for the various zones the future population of each zone as well as that of the entire city when fully developed can be easily worked out. The population density is generally expressed as the number of persons per hectare.

For example in the residential zone of a city the maximum number of tenements to be allowed is 1000 per hectare. Assuming 4 persons per tenement, the population of this zone, when fully developed will be about 4000 per hectare. In the same manner the future population of other zones of the city when fully developed may also be obtained.

(10) Ratio and Correlation Method:

This method is based on the hypothesis that the population growth of a small area is related, to some extent, to the population growth of a large area. Thus the rate of population growth of a town or city is related, to some extent, to the rate of population growth of State or Nation. Hence it is possible to estimate the population of a town or city under consideration by considering the rate of population growth of State or Nation.

In order to predict the future population of a town or city by this method different techniques may be adopted as indicated below:

(1) The ratios of the known populations of the town or city and those of the entire State or Nation for a number of corresponding’ past successive decades (or census) are computed. These ratios are plotted against the respective years of record and a smooth curve is drawn through the plotted points.

The curve is then extrapolated to obtain the values of these ratios for the future years. The ratio for any future year obtained from the extrapolated curve when multiplied by the prospective population of the entire State or Nation for that future year gives the prospective population of the town or city for the same future year.

(2) The ratio of the population of the town or city at the last census and the population of the entire State or Nation at the same last census is worked out and this ratio is adopted for predicting the future population of the town or city.

Thus by multiplying the prospective population of the entire State or Nation for any future year by this ratio the prospective population of the town or city for the same future year may be obtained. It may, however, be noted that in this case a constant ratio is adopted for obtaining the prospective population of the town or city for any desired future year.

(3) The ratios of the known populations of the town or city and those of the entire State or Nation for a number of corresponding past successive decades (or census) are computed and the average of these ratios is worked out, which is adopted for predicting the future population of the town or city.

Thus by multiplying the prospective population of the entire State or Nation for any future year by this average ratio the prospective population of the town or city for the same future year may be obtained. Again in this case also a constant ratio is adopted for obtaining the prospective population of the town or city for any desired future year.

Some of the advantages of this method are as indicated below:

(i) In this method in addition to local factors affecting the population growth, regional or national factors affecting the population growth are also included.

(ii) The population forecasts for State or Nation are usually carried out by careful considerations.

(iii) As compared to small areas the population forecasts of large areas are generally more reliable.

However, the ratio and correlation method would be useful for the areas whose population growth in the past has been fairly consistent with that of the State or Nation.